Hunterbackup307

Venturi meters are flow measurement instruments which use a converging section of pipe to give an increase in the flow velocity and a corresponding pressure drop from which the flowrate can be deduced. They have been in common use for many years, especially in the water supply industry.

• Rumus Venturi Meter Indicator
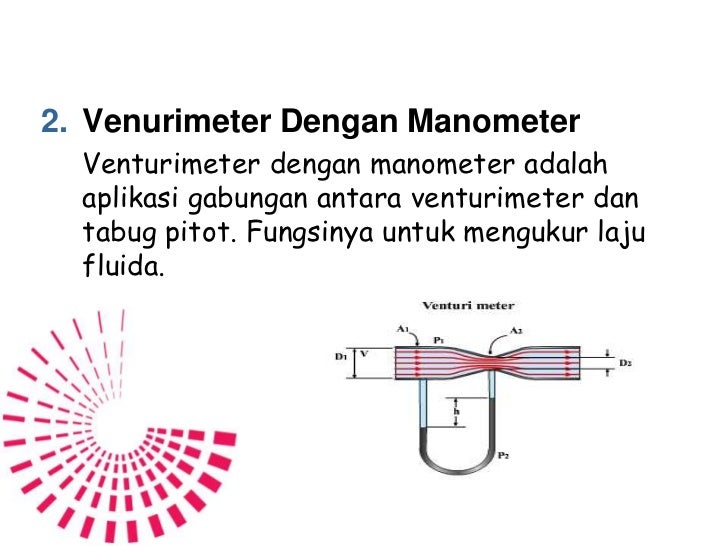
• Rumus Venturi Meter Dengan Manometer
• Rumus Venturi Meter Finger Pulse Oximeter

Makalah Fisika Tabung Venturi Dan Tabung Pitot Pdf Free Download. Soal Venturi Meter Icpns. Perhatikan Gambar Venturimeter Tanpa Manometerdi Bawah Ini A1. 91936548 Tabung Venturi Dan Tabung Pitot Ppt Pdf Document. Hukum Bernoulli Rumus Bunyi Contoh Soal Pembahasan Lengkap. Ka mau nanya kalau rumus venturi itu bisa diterapin buat mencari v didalam pipa yg alirannya steady ga? Atau rumus v itu hanya untuk di venturi aja? Unknown 3 April 2018 04.09. Newbie 18 April 2018 20.42. Makasih gan rumus venturimeter dengan manometernya. Venturimeter dapat dipakai untuk mengukur laju aliran fluida, misalnya menghitung laju aliran air atau minyak yang mengalir melalui pipa.Venturimeter digunakan sebagai pengukur volume fluida misalkan minyak yang mengalir tiap detik. Venturimeter adalah sebuah alat yang bernama pipa venturi.

1. Makalah venturimeter fisika kelas XI Percobaan Venturimeter.
2. Tag: rumus venturimeter. Oleh dosenpendidikan Diposting pada. Suatu zat yang mempunyai kemampuan mengalir dinamakan Fluida.

The classical Venturi meter, whose use is described in ISO 5167-1: 1991, has the form shown in Figure 1

Figure 1. Classical Vetituri meter design. (From B. S. 7405 (1991) Fig. 3.1.4, with permission of B.S.I.)

For incompressible flow if the Bernoulli Equation is applied between two planes of the tappings,

where p, ρ and ū are the pressure, density and mean velocity and the subscripts ₁ and ₂ refer to the upstream and downstream (throat) tapping planes.

From continuity

whereis the volumetric flowrate and D and d the pipe and throat diameters.

Combining Eqs. (1) and (2)

where β is the diameter ratio, d/D. In reality, there is a small loss of total pressure, and the equation is multiplied by the discharge coefficient, C, to take this into account:

where Δp is the differential pressure (≡p₁ − p₂). The discharge coefficient of a Venturi meter is typically 0.985, but may be even higher if the convergent section is machined. Discharge coefficients for uncalibrated Venturi meters, together with corresponding uncertainties, are given in ISO 5167-1: 1991.

If the fluid being metered is compressible, there will be a change in density when the pressure changes from p₁ to p₂ on passing through the contraction. As the pressure changes quickly, it is assumed that no heat transfer occurs and because no work is done by or on the fluid, the expansion is isentropic. The expansion is almost entirely longitudinal and an expansibility factor, ε, can be calculated assuming one-dimensional flow of an ideal gas:

where τ is the pressure ratio, p₂/p₁, and κ the isentropic exponent. The expansibility factor is applied to the flow equation in the same way as the discharge coefficient.

Various forms of construction of a Venturi meter are employed, depending on size, but all are considerably more expensive than the orifice plate. However, because most of the differential pressure is recovered by means of the divergent outlet section, the Venturi causes less overall pressure loss in a system and thus saves energy: the overall pressure loss is generally between 5 and 20 per cent of the measured differential pressure. The Venturi meter has an advantage over the orifice plate in that it does not have a sharp edge which can become rounded; however, the Venturi meter is more susceptible to errors due to burrs or deposits round the downstream (throat) tapping.

The lengths of straight pipe required upstream and downstream of a Venturi meter for accurate flow measurement are given in ISO 5167-1: 1991. These are shorter than those required for an orifice plate by a factor which can be as large as 9. However, Kochen et al. show that the minimum straight lengths between a single upstream 90° bend and a Venturi meter in the Standard are too short by a factor of about 3.

REFERENCES

British Standards Institution (1991) Guide to selection and application of flowmeters for the measurement of fluid flow in closed conduits, BS 7405.

International Organization for Standardization, Measurement of fluid flow by means of pressure differential devices—Part 1: Orifice plates, nozzles and Venturi tubes inserted in circular cross-section conduits running full. ISO 5167-1: 1991.

Kochen, G., Smith, D. J. M., and Umbach, A. (1989) Installation effects on Venturi tube flowmeters, Intech Engineers Notebook, October 1989,41-43.

References

1. British Standards Institution (1991) Guide to selection and application of flowmeters for the measurement of fluid flow in closed conduits, BS 7405.
2. International Organization for Standardization, Measurement of fluid flow by means of pressure differential devices—Part 1: Orifice plates, nozzles and Venturi tubes inserted in circular cross-section conduits running full. ISO 5167-1: 1991.
3. Kochen, G., Smith, D. J. M., and Umbach, A. (1989) Installation effects on Venturi tube flowmeters, Intech Engineers Notebook, October 1989,41-43.

In fluid mechanics, pressure head is the height of a liquid column that corresponds to a particular pressure exerted by the liquid column on the base of its container. It may also be called static pressure head or simply static head (but not static head pressure).

Mathematically this is expressed as:

${\displaystyle \psi =\frac{p}{\gamma }=\frac{p}{\rho g}}$

where

${\displaystyle \psi }$ is pressure head (which is actually a length, typically in units of meters or centimetres of water)

${\displaystyle p}$ is fluid pressure (i.e. force per unit area, typically expressed in pascals)

${\displaystyle \gamma }$ is the specific weight (i.e. force per unit volume, typically expressed in N/m³ units)

${\displaystyle \rho }$ is the density of the fluid (i.e. mass per unit volume, typically expressed in kg/m³)

${\displaystyle g}$ is acceleration due to gravity (i.e. rate of change of velocity, expressed in m/s²).

Note that in this equation, the pressure term may be gauge pressure or absolute pressure, depending on the design of the container and whether it is open to the ambient air or sealed without air.

Head equation[edit]

Pressure head is a component of hydraulic head, in which it is combined with elevation head. When considering dynamic (flowing) systems, there is a third term needed: velocity head. Thus, the three terms of velocity head, elevation head, and pressure head appear in the head equation derived from the Bernoulli equation for incompressible fluids:

${\displaystyle h_v+z_{\text{elevation}}+\psi =C}$

where

${\displaystyle h_v}$ is velocity head,

${\displaystyle z_{\text{elevation}}}$ is elevation head,

${\displaystyle \psi }$ is pressure head, and

${\displaystyle C}$ is a constant for the system

Practical uses for pressure head[edit]

Fluid flow is measured with a wide variety of instruments. The venturi meter in the diagram on the left shows two columns of a measurement fluid at different heights. The height of each column of fluid is proportional to the pressure of the fluid. To demonstrate a classical measurement of pressure head, we could hypothetically replace the working fluid with another fluid having different physical properties.

For example, if the original fluid was water and we replaced it with mercury at the same pressure, we would expect to see a rather different value for pressure head. In fact the specific weight of water is 9.8 kN/m³ and the specific weight of mercury is 133 kN/m³. So, for any particular measurement of pressure head, the height of a column of water will be about [133/9.8 = 13.6] 13.6 times taller than a column of mercury would be. So if a water column meter reads '13.6 cm H₂O', then an equivalent measurement is '1.00 cm Hg'.

Rumus Venturi Meter Indicator

This example demonstrates why there is some confusion surrounding pressure head and its relationship to pressure. Scientists frequently use columns of water (or mercury) to measure pressure (manometric pressure measurement), since for a given fluid, pressure head is proportional to pressure. Measuring pressure in units of 'mm of mercury' or 'inches of water' makes sense for instrumentation, but these raw measurements of head must frequently be converted to more convenient pressure units using the equations above to solve for pressure.

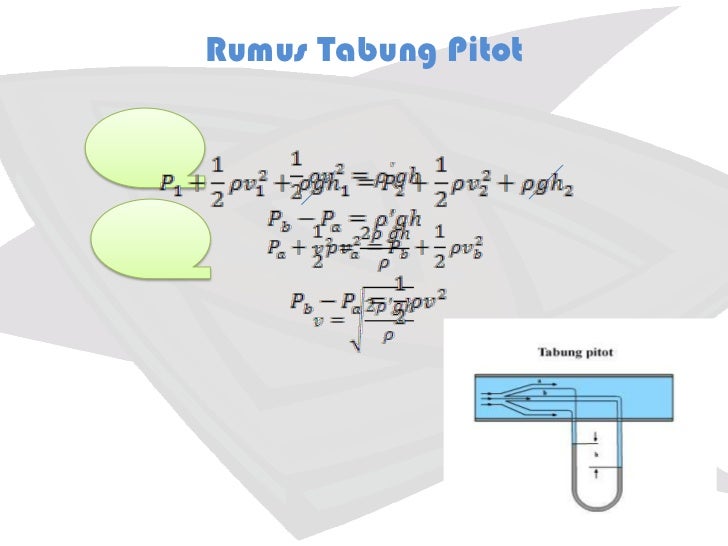
In summary pressure head is a measurement of length, which can be converted to the units of pressure (force per unit area), as long as strict attention is paid to the density of the measurement fluid and the local value of g.

Implications for gravitational anomalies on ${\displaystyle \psi }$[edit]

We would normally use pressure head calculations in areas in which ${\displaystyle g}$ is constant. However, if the gravitational field fluctuates, we can prove that pressure head fluctuates with it.

• If we consider what would happen if gravity decreases, we would expect the fluid in the venturi meter shown above to withdraw from the pipe up into the vertical columns. Pressure head is increased.
• In the case of weightlessness, the pressure head approaches infinity. Fluid in the pipe may 'leak out' of the top of the vertical columns (assuming ${\displaystyle p>0}$).
• To simulate negative gravity, we could turn the venturi meter shown above upside down. In this case gravity is negative, and we would expect the fluid in the pipe to 'pour out' the vertical columns. Pressure head is negative (assuming ${\displaystyle p>0}$).
• If and ${\displaystyle g>0}$, we observe that the pressure head is also negative, and the ambient air is sucked into the columns shown in the venturi meter above. This is called a siphon, and is caused by a partial vacuum inside the vertical columns. In many venturis, the column on the left has fluid in it (${\displaystyle \psi >0}$), while only the column on the right is a siphon ().
• If and , we observe that the pressure head is again positive, predicting that the venturi meter shown above would look the same, only upside down. In this situation, gravity causes the working fluid to plug the siphon holes, but the fluid does not leak out because the ambient pressure is greater than the pressure in the pipe.
• The above situations imply that the Bernoulli equation, from which we obtain static pressure head, is extremely versatile.

Applications[edit]

Static[edit]

A mercury barometer is one of the classic uses of static pressure head. Such barometers are an enclosed column of mercury standing vertically with gradations on the tube. The lower end of the tube is bathed in a pool of mercury open to the ambient to measure the local atmospheric pressure. The reading of a mercury barometer (in mm of Hg, for example) can be converted into an absolute pressure using the above equations.

If we had a column of mercury 767 mm high, we could calculate the atmospheric pressure as (767 mm)•(133 kN/m³) = 102 kPa. See the torr, millimeter of mercury, and pascal (unit) articles for barometric pressure measurements at standard conditions.

Differential[edit]

Rumus Venturi Meter Dengan Manometer

The venturi meter and manometer is a common type of flow meter which can be used in many fluid applications to convert differential pressure heads into volumetric flow rate, linear fluid speed, or mass flow rate using Bernoulli's principle. The reading of these meters (in inches of water, for example) can be converted into a differential, or gauge pressure, using the above equations.

Velocity head[edit]

The pressure of a fluid is different when it flows than when it is not flowing. This is why static pressure and dynamic pressure are never the same in a system in which the fluid is in motion. This pressure difference arises from a change in fluid velocity that produces velocity head, which is a term of the Bernoulli equation that is zero when there is no bulk motion of the fluid. In the picture on the right, the pressure differential is entirely due to the change in velocity head of the fluid, but it can be measured as a pressure head because of the Bernoulli principle. If, on the other hand, we could measure the velocity of the fluid, the pressure head could be calculated from the velocity head. See the Derivations of Bernoulli equation.

See also[edit]

• Hydraulic head or velocity head, which includes a component of pressure head

References[edit]

External links[edit]

Rumus Venturi Meter Finger Pulse Oximeter